draw binary search tree practice

Latest Binary Search Tree MCQ Objective Questions

Binary Search Tree MCQ Question 1:

What will be post order traversal of a binary Tree T, if preorder and inorder traversals of T are given by ABCDEF and BADCFE respectively?

1. BEFDCA
2. BFDECA
3. BCFDEA
4. BDFECA

Answer (Detailed Solution Below)

Option 4 : BDFECA

The correct answer is option 4.

Concept:

The given data,

preorder=ABCDEF

In order = BADCFE

Tree traversal
Method Sequence	Inorder	Preorder	Postorder
	Left Sub-tree	Root	Left Sub-tree
	Root	Left Sub-tree	Right Sub-tree
	Right Sub-tree	Right Sub-tree	Root

The binary tree for the traversal is,

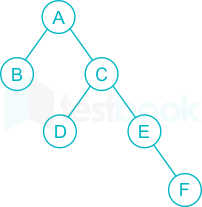
Post order for the above tree is,

BDFECA

Hence the correct answer isBD FECA.

Binary Search Tree MCQ Question 2:

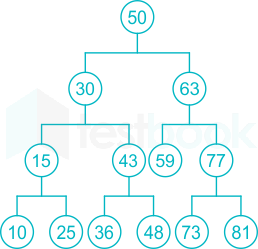
Consider the given binary search tree, if the root node will be deleted, the new root can be -

1. 30 or 63
2. 43 or 48
3. 63 or 81
4. 48 or 59

Answer (Detailed Solution Below)

Option 4 : 48 or 59

The correct answer is option 4.

Concept:

Binary search tree:

A binary search tree (BST) is a binary tree in which each node has a Comparable key (and an associated value) that is greater than the keys in all nodes in that node's left subtree and less than the keys in all nodes in that node's right subtree.

Deletion of nodes in binary search tree:

A node to be deleted

1. No children then simply delete it.
2. Only one child then connects to the child subtree to its grandparent.
3. Both children(subtrees) then:
   1. Replace with its INORDER SUCCESSOR (Minimum node of the right subtree). or
   2. Replace with its INORDER PREDECESSOR (Maximum node of the left subtree).

Explanation:

The given BST, A node to be deleted has a root node i.e  50.

From deletion algorithm of rule 3.1 or 3.2 applicable for the given condition.

Replace with its INORDER SUCCESSOR:

Here is the minimum node of the right subtree is the node= 59

Replace with its INORDER PREDECESSOR:

Here the Maximum node of the left subtree is the node= 48.

Hence the correct answer is48 or 59.

Binary Search Tree MCQ Question 3:

If we delete Node 15 from the given BST the pre-order traversal of the resultant tree is:

1. 20, 10, 2, 16, 12, 17, 19, 30, 27
2. 20, 10, 12, 2, 17, 16, 19, 30, 27
3.  20, 2, 10, 16, 12, 17, 19, 30, 27
4. 20, 12, 10, 2, 17, 16, 19, 30, 27

Answer (Detailed Solution Below)

Option 4 : 20, 12, 10, 2, 17, 16, 19, 30, 27

The correct answer is option 4.

Concept:

Pre-Order traversal:-Root - Left child - Right child.

Binary search tree:​

A binary search tree arranges its elements in a certain order. In a Binary search tree, the value of the left node must be less than the value of the parent node, and the value of the right node must be bigger than the value of the parent node. This rule is applied recursively to the root's left and right subtrees.

From the given BSTIf we delete Node 15 then we will get two BST are,

20, 12, 10, 2, 17, 16, 19, 30, 27

20, 16, 10, 2, 12, 17, 19, 30, 27

20, 16, 10, 2, 12, 17, 19, 30, 27 and 20, 12, 10, 2, 17, 16, 19, 30, 27 are preorder for the given BST. Only 2 possible trees are possible after the deletion of  15 from a given BST.

Hence the correct answer is20, 12, 10, 2, 17, 16, 19, 30, 27.

Binary Search Tree MCQ Question 4:

Consider the following binary search tree T. A new node of value 12 is inserted into the T. What is the height of the tree after inserting node 12?

Hint:

The height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.

1. 1
2. 2
3. 3
4. 4

Answer (Detailed Solution Below)

Option 4 : 4

The correct answer is option 4.

Concept:

Binary search tree:

A rooted binary tree data structure whose internal nodes each hold a key higher than all the keys in the node's left subtree and fewer than those in the node's right subtree is known as a binary search tree.

A node 12 inserted  tree becomes,

Height:

The height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.

Height of the binary tree is= 4.

Hence the correct answer is 4.

Binary Search Tree MCQ Question 5:

Which of the following is a height of a given binary tree?

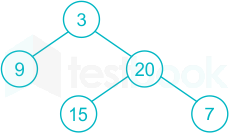
Hint:

The height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.

1. 1
2. 2
3. 3
4. 4

Answer (Detailed Solution Below)

Option 2 : 2

The correct answer isoption 2.

Concept:

Binary tree:

A binary tree is a tree in which no node can have more than two children. Every binary tree has parents, children, siblings, leaves, and internal nodes.

Height of a binary tree:

The height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.

Explanation:

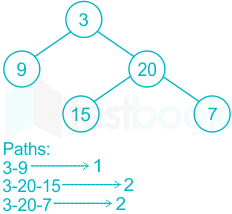
Hence the correct answer is 2.

Top Binary Search Tree MCQ Objective Questions

Which of the following is/are correct in-order traversal sequence(s) of binary search tree(s)?

I. 3, 5, 7, 8, 15, 19, 25

II. 5, 8, 9, 12, 10, 15, 25

III. 2, 7, 10, 8, 14, 16, 20

IV. 4, 6, 7, 9 18, 20, 25

1. I and IV only
2. II and III only
3. II and IV only
4. II only

Answer (Detailed Solution Below)

Option 1 : I and IV only

Statement I: 3, 5, 7, 8, 15, 19, 25

It doesn't violate Binary search tree property and hence it is the correct order of traversal.

Statement II: 5, 8, 9, 12, 10, 15, 25

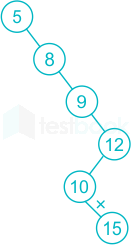
15 is left of 12 which violates binary search tree property.

Statement III:2, 7, 10, 8, 14, 16, 20

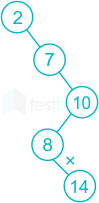
14 is left of 10 which violates binary search tree property.

Statement IV: 4, 6, 7, 9 18, 20, 25

It doesn't violate Binary search tree property and hence it is the correct order of traversal.

The preorder traversal sequence of a binary search tree is 30, 20, 10, 15, 25, 23, 39, 35, 42. Which one of the following is the postorder traversal sequence of the same tree?

1. 10, 20, 15, 23, 25, 35, 42, 39, 30
2. 15, 10, 25, 23, 20, 42, 35, 39, 30
3. 15, 20, 10, 23, 25, 42, 35, 39, 30
4. 15, 10, 23, 25, 20, 35, 42, 39, 30

Answer (Detailed Solution Below)

Option 4 : 15, 10, 23, 25, 20, 35, 42, 39, 30

The correct answer is "option 4".

CONCEPT:

A Binary Search Tree (BST) is also known as an ordered tree or sorted binary tree.

It is a binary tree with the following properties:

1. The left sub-tree of a node contains only nodes with key-value lesser than the node's key value.

2.  The right subtree of a node contains only nodes with a key-value greater than the node's key value.

There are three types of traversal:

1. In-order traversal: In this traversal, the first left node will traverse, the root node then the right node will get traversed.

2. Pre-order traversal: In this traversal, the first root node will traverse, the left node then the right node will get traversed.

3. Post-order traversal: In this traversal, the First left node will traverse, the right node then the root node will get traversed.

The in-order traversal of the Binary search tree always returns key values in ascending order.

EXPLANATION:

The pre-order traversal of given BST is:

30, 20, 10, 15, 25, 23, 39, 35, 42.

So, the In-order traversal of the BST is:

10, 15, 20, 23, 25, 30, 35, 39, 42.

The Binary Search Tree is:

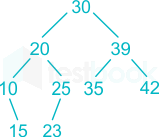
So the post-order traversal of the tree is:

15, 10, 23, 25, 20, 35, 42, 39, 30

Hence, the correct answer is "option 4".

The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree?

1. 3
2. 4
3. 5
4. 6

Answer (Detailed Solution Below)

Option 1 : 3

The correct answer is option 1

Concept:

A binary search tree (BST) is a node-based binary tree data structure and it follows the following points

1. Left sub-tree nodes key value will exist only if lesser than the parent node key value.
2. Right sub-tree nodes key value will exist only if greater than the parent node key value.
3. Left sub-tree and Right sub-tree must be a Binary search tree.
   

Explanation:

Step 1 : First 10 comes and now that is the Root node.

Step 2: Now 1 came and 1 < 10 then insert Node 1 to the Left of Node 10.

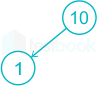
Step 3: Now 3 came and 3 < 10 go to the Left of

Node 10 and check 3 > 1 then insert Node 3  to the Right of Node  1.

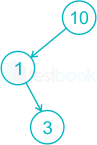
Step 4 : Now 5 came  and 5 < 10 go to the  Left  of

Node 10 and check 5 > 1 go to the Right of Node 1 then check  5 > 3 then insert Node 5 to the Right of Node 3.

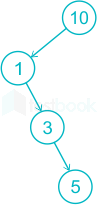
Step 5 : Now 15 came and 15 > 10 then insert Node 15 to the Right of Node 10.

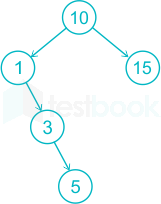
Step 6: Now 12 came and 12 > 10  go to theRight of  Node 10 and check 15 > 12 then insert Node 12  to the Left of Node 15.

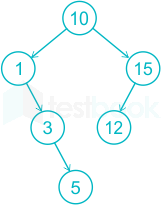
Step 7:Now 16 came and 16 > 10 go to the Right of

10 and check 16 > 15 then insert 16  to the Right of Node 15.

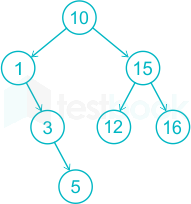
After step 7,  we can count the height of the tree as 3.

Important Points

Follow the longest path in the tree and count the edges that are height.

Tips To Learn:

Leftsub-tree(key)<Node(key)<Right sub-tree(key)

Node(key): Parent node ofLeftsub-tree and Right sub-tree

Suppose the numbers 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are inserted in that order into an initially empty binary search tree. The binary search tree uses the reversal ordering on natural numbers i.e. 9 is assumed to be smallest and 0 is assumed to be largest. The in-order traversal of the resultant binary search tree is

1. 9, 8, 6, 4, 2, 3, 0, 1, 5, 7
2. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
3. 0, 2, 4, 3, 1, 6, 5, 9, 8, 7
4. 9, 8, 7, 6, 5, 4, 3, 2, 1, 0

Answer (Detailed Solution Below)

Option 4 : 9, 8, 7, 6, 5, 4, 3, 2, 1, 0

Insert 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 in empty binary search tree by using reverser ordering

Binary search tree:

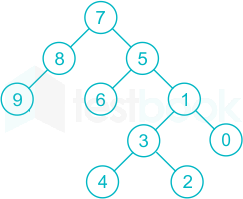
Inorder traversal = 9, 8, 7, 6, 5, 4, 3, 2, 1, 0

Tips and Trick:

In-order of the binary tree is always sorted in ascending order but binary search tree uses the reversal ordering on natural numbers

Therefore it is sorted in descending order:

Consider the following two statements.

1. A binary tree T is full if each node is either a leaf or possesses exactly two child nodes.

2. A binary tree T with n levels is complete if all levels except possibly the last are completely full, and the last level has all its nodes to the left side.

Which statement is/are TRUE

1. Only 1
2. Only 2
3. 1 and 2
4. Neither 1 nor 2

Answer (Detailed Solution Below)

Option 3 : 1 and 2

Explanation:

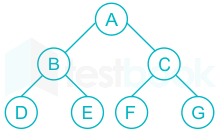
Statement 1:  TRUE

It is definition of binary tree, which is full, this is also called as perfect binary tree.

Example of Binary tree which is FULL:

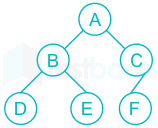
Statement 2:  TRUE

It is definition of binary tree which is complete.

Example of Binary tree which is COMPLETE:

What are the worst-case complexities of insertion and deletion of a key in a binary search tree?

1. θ (log n) for both insertion and deletion
2. θ (n) for both insertion and deletion
3. θ (n) for insertion and θ (log n) for deletion
4. θ (log n) for insertion and θ (n) for deletion

Answer (Detailed Solution Below)

Option 2 : θ (n) for both insertion and deletion

Concepts:

Minimum height of the tree is when all the levels of the binary search tree (BST) are completely filled.

Maximum height of the BST is the worst case when nodes are in skewed manner.

Formula:

Minimum height of the BST with n nodes is ⌈log2 (n + 1)⌉ - 1

The maximum height of the BST with n nodes is n - 1.

BST with a maximum height:

Insertion:

Traverser the BST to the maximum height

Worst-case time complexity of Insertion = θ (n - 1) ≡ θ (n)

Deletion:

Traverser the BST to the maximum height

Worst-case time complexity of  = θ (n - 1) ≡ θ (n)

A binary search tree T contains n distinct elements. What is the time complexity of picking an element in T that is smaller than the maximum element in T?

1. Θ(1)
2. Θ(n log n)
3. Θ(log n)
4. Θ(n)

Answer (Detailed Solution Below)

Option 1 : Θ(1)

Explanation:

• If an element in a binary search tree is smaller than any other element in the binary search tree then it is smaller than the maximum element.
• All the elements in the binary search tree is distinct.
• Compare only two elements in the binary search tree to find such elements.
• Therefore time complexity is θ(1).

To arrange a binary search tree in ascending order, we need

1. Post order traversal only
2. In order traversal only
3. Pre order traversal only
4. Post order traversal and Pre order traversal only

Answer (Detailed Solution Below)

Option 2 : In order traversal only

Random binary search tree

Post-order traversal is 23, 18, 27, 25, 10, 60, 80, 70, 30.

In-order traversal traversal is 10, 18, 23, 25, 27, 30, 60, 70, 80

Preorder traversal is 30, 10, 25, 18, 23, 27, 70, 60 ,80

Therefore, to arrange a binary search tree in ascending order, we needIn order traversal only

The number of ways in which the numbers 1, 2, 3, 4, 5, 6, 7 can be inserted in an empty binary search tree, such that the resulting tree has height 6, is.

Note: The height of a tree with a single node is 0.

Answer (Detailed Solution Below) 64

Resulting tree must have height = 6

So, root must be either 1 or 7

For node 1 (also for node 7):

Possible permutations are = \(\frac{{6!}}{{6!0!}} = 1\)

For node 2 (also for node 6):

Possible permutations are =\(\frac{{6!}}{{5!1!}} = 6\)

For node 3(also for node 5):

Possible permutations are =\(\frac{{6!}}{{4!2!}} = 15\)

For node 4:

Possible permutations are =\(\frac{{6!}}{{3!3!}} = 20\)

Number of ways in which nodes are inserted to get height 6 = 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64

The program written for binary search, calculates the midpoint of the span as mid : = (Low + High)/2. The program works well if the number of elements in the list is small (about 32,000) but it behaves abnormally when the number of elements is large. This can be avoided by performing the calculation as:

1. mid : = (High - Low)/2 + Low
2. mid : = (High - Low + 1)/2
3. mid : = (High - Low)/2
4. mid : = (High + Low)/2

Answer (Detailed Solution Below)

Option 1 : mid : = (High - Low)/2 + Low

The correct answer is option 1.

Key Points

• In a general scenario,  binary search mid-value computed with, mid=(low+high)/2.
• However, with a vast list of elements, "high" would be a very large value. As a result, it's possible that it's beyond the Integer limit. It's known as an integer overflow.
• To stop this Integer overflow, the 'mid' value can also be determined using,mid  = (High - Low)/2 + Low
• Integer overflow is never an issue with this form.

Explanation

mid : = (High - Low)/2 + Low

mid : =  High/2 - Low/2 + low

mid : =   (High + Low)/2

Alternate Method

• Option D is removed because it is the same as the incorrect option.

• Taking into account The low index is 10, while the high index is 15.

• Option B returns a mid-index of 3 that is not even in the sub-array index.

• Choice C returns a mid-index of 2 that isn't even in the sub-array index.

• Option A is the best solution.

Hence the correct answer is mid : = (High - Low)/2 + Low .

The following is the sequence of insertion in a binary search tree.

45,65,35,40,33,70,60,75,69

How many numbers of nodes in Left Sub Tree (LST) and Right Sub Tree (RST) of Root node.

1. LST – 3, RST-5
2. LST – 6, RST-2
3. LST – 2, RST-6
4. LST – 5, RST-3

Answer (Detailed Solution Below)

Option 1 : LST – 3, RST-5

Concept:

In binary search tree

• Left sub tree (LST) of every node should contains only nodes with key value less than the node's key
• Right sub tree (RST ) of every node should contains only nodes with key values greater or equal  than the node's key

Explanation:

BST tree after inserting all the nodes ( values )

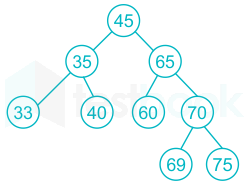
∴ LST = 3 and RST = 5

Consider the following statements:

I. The smallest element in a max-heap is always at a leaf node

II. The second largest element in a max-heap is always a child of the root node

III. A max-heap can be constructed from a binary search tree in Θ(n) time

IV. A binary search tree can be constructed from a max-heap in Θ(n) time

Which of the above statements are TRUE?

1. I, II and III
2. I, II and IV
3. I, III and IV
4. II, III and IV

Answer (Detailed Solution Below)

Option 1 : I, II and III

Max-heap:

• Smallest element (12) of the max heap is always at the leaf.
• Second largest element (25) in a max heap is always a child of the root node

Binary Search Tree:

INORDER: 14, 15, 18, 20, 22, 23, 25, 30

Traversal time complexity = O(n)

Store the element in an array in reverse order

Index	0	1	2	3	4	5	6	7
Array elements	30	25	23	22	20	18	15	14

Filling the array in reverse order. Time complexity = Θ(n)

Total time complexity = Θ(n) + Θ(n) = Θ(n)

MAX heap:

Statement I, II and III are correct

Important Points:

A binary search tree can be constructed from a max heap in Θ(n²) time

Assume that distinct elements are present

While inserting the elements 71, 65, 84, 69, 67, 83 in an empty binary search tree (BST) in the sequence shown, the element in the lowest level is

1. 65
2. 67
3. 69
4. 83

Answer (Detailed Solution Below)

Option 2 : 67

In a BST, inorder traversal is always sorted.

Hence 67 is at lowest level.

The worst case running time to search for an element in a balanced binary search tree with n2ⁿ elements is

1. Θ (n log n)
2. Θ (n2ⁿ)
3. Θ (n)
4. Θ (log n)

Answer (Detailed Solution Below)

Option 3 : Θ (n)

The correct answer is "option 3".

CONCEPT:

There are three types of complexities:

1. Worst case: It is the maximum running time taken by any algorithm.

2. Average case: It is the average running time taken by any algorithm.

3. Best case: It is the minimum running time taken by any algorithm.

EXPLANATION:

Since the worst-case running time to search 'n' elements in a balanced Binary Search Tree (BST) is (log₂n).

If the number of elements is (n2ⁿ ) then,

Search time will be: T(n) = (log₂n.2ⁿ )

Since log₂(A.B) = log₂A + log₂B

∴T(n) =log₂n + log₂2ⁿ

∴T(n)  = log₂n + n.log22 = log2n + n

T(n) = O(n)

Hence the correct answer is "option 3".

Consider the following binary search tree T given below. Which node contains the fourth smallest element in T ?

1. Q
2. V
3. W
4. X

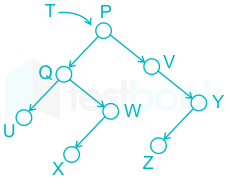
Answer (Detailed Solution Below)

Option 3 : W

The correct answer is option 3.

Key Points

• The binary search tree's in-order traverse provides the ascending order of the elements.
• UQXWPVZY is the in-order traversal of this tree.
• Therefore the fourth-smallest element is the 4th in order element, W.

​
∴ Hence the correct answer is W.

​ Additional Information

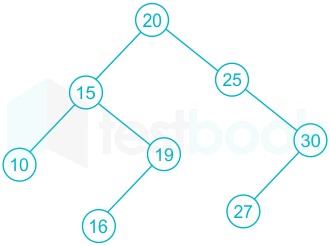
The above tree in order is 10, 15, 16, 19, 20, 25, 27, 30. So the 4^thsmallest element is 19. So the 4th smallest element is W.

Following numbers(items) are inserted in order into binary search tree.

40,60,50,33,55,11

Then the number of items in left and right subtrees of the root are _______

1. (3,3)
2. (2,3)
3. (3,2)
4. (2,4)

Answer (Detailed Solution Below)

Option 2 : (2,3)

Concept:

Binary search tree is a tree where the left subtree contains all the nodes smaller or equal to the root while right subtree contains the nodes greater than the root.

Explanation:

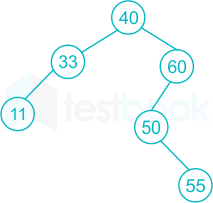
Here number of items in the left subtree of root are 2 and number of items in the right subtree of root are 3.

Tips and Tricks:

Sort: 11 33 40 50 55 60

Since 40 is the root to the left of 40 two nodes and to the right of 40, 3 nodes

Suppose we have a balanced binary search tree T holding n numbers. We are given two numbers L and H and wish to sum up all the numbers in T that lie between L and H.

Suppose there are m such numbers in T. If the tightest upper bound on the time to compute the sum is 0(n^a log^bn + m^c log^d n), the value of a + 10b + 100c + 1000d is

____.

Answer (Detailed Solution Below) 110

In worst case for finding L and H it will take O (log n) time as the given tree is balanced binary search tree.

There are m elements between L and H. So, to traverse m element it will take O(m) time (traversal algorithm given below).

Total time complexity

O(m + log₂n)

Comparing with 0(n^a log^bn + m^c log^d n)

∴ a = 0, b = 1, c = 1, d = 0

a + 10b + 100c + 1000d = 0+(10 × 1) + (100 × 1) + (1000 × 0)

∴ a + 10b + 100c + 1000d = 110.

Consider the binary search tree with n elements. The time required to search given element is: _______

1. θ (log n)
2. θ (n log n)
3. θ (n²)
4. θ (n² log n)

Answer (Detailed Solution Below)

Option 1 : θ (log n)

Concept:

In Binary search tree, searching of a given element depends on height of BST.

Explanation:

Height of BST in Worst case: O ( n )

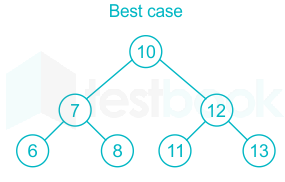
Height of BST in Best case: Ω ( log n )

Height of BST in Average case: Ө ( log n )

Hence option 1 is the correct answer.

A binary search tree is used to locate the number 43. Which one of the following probe sequence is not possible?

1. 61, 52, 14, 17, 40, 43
2. 10, 65, 31, 48, 37, 43
3. 81, 61, 52, 14, 41, 43
4. 17, 77, 27, 66, 18, 43

Answer (Detailed Solution Below)

Option 4 : 17, 77, 27, 66, 18, 43

Concept:

In binary search tree in-ordered traversal is always sorted, when looking for a key in a tree (or a place to insert a new key), they traverse the tree from root to leaf, making comparisons to keys stored in the nodes of the tree and deciding, on the basis of the comparison, to continue searching in the left or right subtrees.

Option 4: Probe sequence is not possible

18 is right of 27, since this probe sequence violates binary search tree definition and hence it is not possible

What will be post order traversal of a binary Tree T, if preorder and inorder traversals of T are given by ABCDEF and BADCFE respectively?

1. BEFDCA
2. BFDECA
3. BCFDEA
4. BDFECA

Answer (Detailed Solution Below)

Option 4 : BDFECA

The correct answer is option 4.

Concept:

The given data,

preorder=ABCDEF

In order = BADCFE

Tree traversal
Method Sequence	Inorder	Preorder	Postorder
	Left Sub-tree	Root	Left Sub-tree
	Root	Left Sub-tree	Right Sub-tree
	Right Sub-tree	Right Sub-tree	Root

The binary tree for the traversal is,

Post order for the above tree is,

BDFECA

Hence the correct answer isBD FECA.

williamguall1969.blogspot.com

Source: https://testbook.com/objective-questions/mcq-on-binary-search-tree--5eea6a1139140f30f369eb9e

Share this post